Predicting Yankee Wins
Fun with the Pythagorean Expectation
If you have read a few of the posts on this blog, it is obvious that I am a baseball fan in general and a Yankees fan in the particular.
Like any other Yankee fan, I hope, and perhaps expect that the Yankees will enter the playoffs. To assess the team’s chances, I run the Yankees’ Pythagorean expectation throughout the season.
At the risk of producing a glazed look in the eyes of those unfortunate enough to read this blog, I will do my best to explain: The Pythagorean expectation is a simple formula used to predict a baseball team’s winning percentage. It’s based on a club’s runs and runs allowed, and was first observed by Bill James, the godfather of sabermetrics. The formula is “Pythagorean” because it is similar to the Pythagorean theorem.
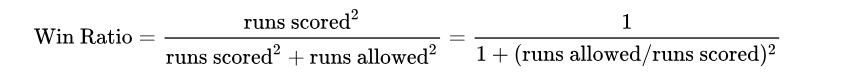
(The Pythagorean Expectation. Source: Wikipedia)
Over the years, researchers modified the original formula, adjusting the exponent from 2.0. Some suggest using an exponent of 1.83. Other researchers suggest using an exponent based on a team’s runs scored, runs allowed and games played. One such formula is the so-called Pythagenpat. Pythagenpat takes the ratio of runs and runs allowed divided by the games played. The ratio is raised to the power of 0.287.
In any event, the Pythagorean expectation is spooky in that and does a remarkably good job of approximating a team’s wins and losses. Want to see evidence of the great programmer in the sky? Play around with the Pythagorean expectation, and you will think that you are witnessing such evidence. Look into the formula’s prescient crystal ball throughout the season and you will provide a good assessment of a club’s end-of-season prospects. Though it’s tough to read anything into the formula at the start of the season, it regresses towards the mean as the season progresses.
The trouble is, there is some leg work required to determine a team’s expected wins. One has to go to a website and find a team’s runs scored and runs allowed, in addition to the number of games played. Then one has to do the math. While it takes 10 minutes or so to assemble the information, do this every week and one has wasted a lot of time. Furthermore, each calculation provides a new vehicle for a miscalculation.
To remedy this, I created the python function below. It scrapes the web to find the latest statistics on the Yankees, then plugs that information into the Pythagorean expectation. It also adjusts the exponent using the Pythagenpat formula. It’s quick to use and saves loads of time over the course of the season.
def pythagoreanNYY():
#Importing libraries
import pandas as pd
import datetime as dt
from bs4 import BeautifulSoup
import requests
#Creating flexible date and time variables.
today = dt.datetime.today()
now = str(today.month) + '/'+ str(today.day)
year = str(today.year)
#Creating URL
url = \
'https://www.baseball-reference.com/teams/NYY/'\
+ year +'.shtml'
#Scraping baseball website for statistics
response = requests.get(url)
if response.status_code == 200:
print("Website Running")
else:
print("Website Down")
#Creating 'Beautiful Soup'
soup = BeautifulSoup(response.content,'lxml')
#Pulling runs scored and runs allowed from soup
stats = soup.find_all('p')[3].get_text().strip\
('Pythagorean W-L:\n\t')
runs_scored = float(stats[7:10])
runs_allowed= float(stats[17:20])
#Calculating games played
wins = []
loss = []
stater =stats[0:6]
for i in stater:
if stater[2] == '-':
winner = stater[0:2]
winner = winner[0]+winner[1]
loser = stater[3:5]
losers = loser[0]+loser[1]
wins.append(winner)
loss.append(losers)
yankee_wins = float(wins[0])
yankee_loss = float(loss[0])
games = yankee_wins + yankee_loss
#Calculating exponent using Pythaganpat
exponent = ((runs_scored + runs_allowed)/games) ** .287
#Calculating Pythagorean expectation
#Calculating expected wins & expected losses
Pythagorean_Expectation= \
round(1/(1+((runs_allowed/runs_scored)**exponent)),4)
Expected_Wins = round(Pythagorean_Expectation * 162,4)
Expected_losses = (162- Expected_Wins)
print("NYY Pythagorean Expectation as of {d}:\
{p}".format(d= now,p= Pythagorean_Expectation))
print("NYY Expected Wins as of {d}:\
{p}".format(d= now,p= int(round(Expected_Wins,0))))
print("NYY Expected Losses as of {d}: \
{p}".format(d= now,p= round(Expected_losses)))
(The above function scrapes the web for relevant data and calculates the New York Yankees’ Pythagorean expectation.)
When we run the function, we get the Yankees Pythagorean win ratio, in addition to the expected wins and losses.
Neat, no?

(Though the Yankees should win over 100 games, their 2018 path to the playoffs depends largely on the success of the Red Sox.)
In complete disclosure, I also closely follow Pythagorean expectation for the Boston Red Sox, not because I like Boston, but because I want to keep and eye on the competition. The following function is the same as above, except it scrapes a different page on the Baseball Reference website and provides the same information for the Red Sox:
def pythagoreanBos():
import datetime as dt
from bs4 import BeautifulSoup
import requests
#Creating flexible time VARIABLES
today = dt.datetime.today()
now = str(today.month) + '/'+ str(today.day)
year = str(today.year)
url =\
'https://www.baseball-reference.com/teams/BOS/'\
+ year +'.shtml'
response = requests.get(url)
if response.status_code == 200:
print("Website Running")
else:
print("Website Down")
soup = BeautifulSoup(response.content,'lxml')
stats = soup.find_all('p')[3].get_text().strip\
('Pythagorean W-L:\n\t')
runs_scored = float(stats[7:10])
runs_allowed= float(stats[17:20])
wins = []
loss = []
stater =stats[0:6]
for i in stater:
if stater[2] == '-':
winner = stater[0:2]
winner = winner[0]+winner[1]
loser = stater[3:5]
losers = loser[0]+loser[1]
wins.append(winner)
loss.append(losers)
yankee_wins = float(wins[0])
yankee_loss = float(loss[0])
games = yankee_wins + yankee_loss
exponent = ((runs_scored + runs_allowed)/games) ** .287
Pythagorean_Expectation= \
round(1/(1+((runs_allowed/runs_scored)**exponent)),4)
Expected_Wins = round(Pythagorean_Expectation * 162,4)
Expected_losses = (162- Expected_Wins)
print("BoSox Pythagorean Expectation as of {d}:\
{p}".format(d= now,p= Pythagorean_Expectation))
print("BoSox Expected Wins as of {d}: {p}".format(d= now,p= int(round(Expected_Wins,0))))
print("BoSox Expected Losses as of {d}: {p}".format(d= now,p= round(Expected_losses)))

(The Yankees have some work to do in the second half of the 2018 season if they expect to win the American League East)
Of course, these functions are not without risks. I had to sculpt the code to accommodate the idiosyncrasies of the Baseball Reference website. Any changes in the layout on that website could render the above functions useless. That being said, the code can be easily modified, and we can remedy any problems with a few lines of code.
Note that these functions can be easily modified to scrape every team, and if I have more time this summer, I write one function that covers every team.